



弹性应变工程是一种通过改变材料的相关结构和机械性质来实现调控材料电子结构性质的技术。在过去几十年,这种技术已被广泛应用于半导体行业,以便通过提高硅的载流子迁移率来提高器件的电学性能。然而,传统的半导体单晶体材料由于所能承受的应变非常有限,在很大程度上限制了通过弹性应变调节半导体材料电子特性的能力。
近来二维层状材料得到了极为广泛的关注,其特性表现为面内拥有极强的共价键,而层与层之间仅靠极为微弱的范德瓦尔斯力结合。在二维材料中最引人注目的是石墨烯、六方氮化硼(h-BN )、黑磷(BP)及过渡金属硫化物(TMDs) 中的MoS2, WS2, WSe2等。这些材料拥有各具特色的光学和电子特性。更重要的是这些二维材料通常都能够比体材料承受更大的弹性应变而不损伤。例如,大部分石墨材料在应变为0.1%时会破碎,但单层石墨烯却能承受25%的弹性应变。这使得二维材料成为一个在弹性应变工程中值得探索的重要领域。
最近,纳米中心刘前课题组与中科院半导体所李京波课题组以及亚利桑那州立大学Sefaattin课题组合作,通过褶皱应变调节二维材料ReSe2物理特性取得重要进展,相关工作以“Tuning the Optical, Magnetic, and Electrical Properties of ReSe2 by Nanoscale Strain Engineering”为题,发表在Nanoletters上(http://pubs.acs.org/doi/abs/10.1021/nl504276u)。纳米中心博士生王聪与半导体所博士后杨圣雪为共同第一作者。
纳米中心的课题组在薄膜材料的褶皱制作上积累了丰富经验(Adv. Mater. DIO:10.1002/adma.201200540),为本工作的开展提供了基础。本研究提出在一种新型的过渡金属硫化物二维材料ReSe2中制造褶皱,发现:(1)退化的Eg-like拉曼峰在褶皱区域劈裂成两个峰,同时Ag-like的拉曼峰发生红移;(2)实现荧光光谱的红移,这一现象被第一性原理计算的褶皱区域ReSe2带隙的减小所证实;(3)荧光光谱的强度会高于非褶皱区域,这是由于激光激发的电子空穴对(激子)在“太阳能漏斗效应”下被诱导到应变最大、材料带隙最小的褶皱区域并在褶皱区域完成电子空穴对复合导致的。(4)分析磁力显微镜(MFM)的相位以及振幅的移动,确认原本没有磁性的单层ReSe2被褶皱产生的区域应变诱导磁性,第一性原理计算显示磁性区域的能量要比非磁性区域的小300 meV,同时褶皱区域的ReSe2磁矩从非褶皱区域的0 μB增大到~3.95 μB,很好的证实了MFM测试的结果;(5)I-V曲线显示,在不同应力下的褶皱区域表现出了不同的电学特性。
这些发现表明褶皱在纳米尺度上可以很好的调控二维材料的物理性质,对研发广泛应用于压力传感器、柔性电极、柔性场效应晶体管、太阳能电池和其他光子设备的多功能材料具有促进作用。
上述研究得到了国家自然科学基金以及中科院先导项目的支持。

Figure 1.Magnetic force microscopy measurements on ReSe2 . (a) AFM topography, (b) phase, (c) MFM phase, and (d) MFM amplitude images of monolayer ReSe2 wrinkledflake on gel−film substrate. (e−h) The corresponding profiles in panels a−d.
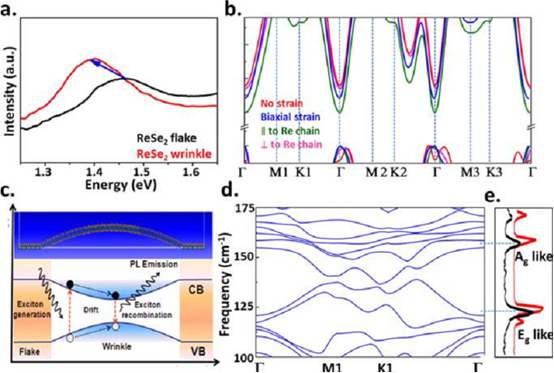
Figure 2.Raman and photoluminescence spectra of strained monolayer ReSe2. (a) Photoluminescence spectra measured on the flat (black) and on the wrinkle (red) regions in the same position of the ReSe2 monolayer. (b) Density functional theory (DFT) calculation performed on unstrained (red), biaxial strain (blue), and strain in parallel (green) and perpendicular (magenta) directions. (c) Schematic diagram of the funnel effect in the ReSe2 wrinkle explaining the enhancement in the integrated PL emission intensity and PL peak position. (d) Phonon dispersion relation calculated from DFT calculations. (e) Raman spectra taken on unstrained (black) and strained (red) ReSe2